十大排序算法实现(Java版)
一. 常用排序算法
1
2
3
4
5
|
int a10 = 99;
int a2 = 0b101;
int a8 = 0143;
int a16 = 0x63;
|
0x01 冒泡排序
原理
比较相邻的元素。如果第一个比第二个大,就交换他们两个。 对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。 针对所有的元素重复以上的步骤,除了最后一个。 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
public static int[] bubbleSort(int[] nums) {
if (nums != null && nums.length > 1) {
int len = nums.length;
int tmp;
for (int i = 1; i <= len; i++) {
for (int j = 0; j < len - i; j++) {
if (nums[j] > nums[j + 1]) {
tmp = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = tmp;
}
}
}
}
return nums;
}
|
0x02 选择排序
原理
第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。
代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
public static int[] selectSort(int[] nums) {
int len = nums.length;
int min, tmp;
for (int i = 0; i < len - 1; i++) {
min = i;
for (int j = i + 1; j < len; j++) {
if (nums[j] < nums[min]) min = j;
}
if (min != i) {
tmp = nums[i];
nums[i] = nums[min];
nums[min] = tmp;
}
}
return nums;
}
|
0x03 插入排序
原理
插入排序是一种最简单的排序方法,它的基本思想是将一个记录插入到已经排好序的有序表中,从而一个新的、记录数增1的有序表。在其实现过程使用双层循环,外层循环对除了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找,并进行移动。
- 时间复杂度
在插入排序中,当待排序数组是有序时,是最优的情况,只需当前数跟前一个数比较一下就可以了,这时一共需要比较N- 1次,时间复杂度为 O(N) 。
最坏的情况是待排序数组是逆序的,此时需要比较次数最多,总次数记为:1+2+3+…+N-1,所以,插入排序最坏情况下的时间复杂度为O(N^2) 。
- 空间复杂度
插入排序的空间复杂度为常数阶O(1)。
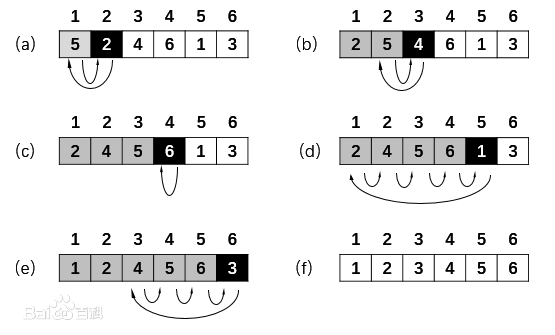
代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
public static int[] insertSort(int[] nums) {
if (nums != null && nums.length > 1) {
int len = nums.length;
for (int i = 1; i < len; i++) {
int candidate = nums[i];
int j = i - 1;
while (j >= 0 && candidate < nums[j]) {
nums[j + 1] = nums[j];
j--;
}
nums[j + 1] = candidate;
}
}
return nums;
}
|
0x04 快速排序
原理
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
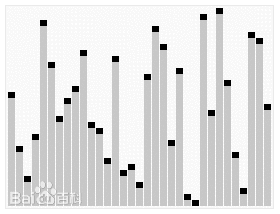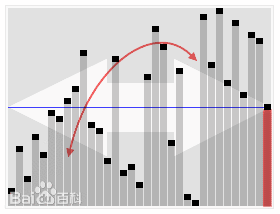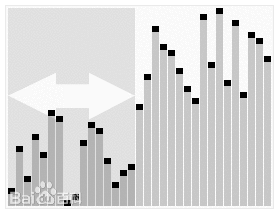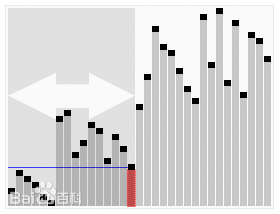
代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
public static int[] quickSort(int[] nums) {
quickSort(nums, 0, nums.length - 1);
return nums;
}
private static void quickSort(int[] nums, int start, int end) {
int i = start;
int j = end;
int key = nums[start];
while (i < j) {
while (i < j && nums[j] > key) {
j--;
}
while (i < j && nums[i] < key) {
i++;
}
if (i < j) {
if (nums[i] == nums[j]) {
i++;
} else {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}
}
if (i - 1 > start)
quickSort(nums, start, i - 1);
if (j + 1 < end)
quickSort(nums, j + 1, end);
}
|
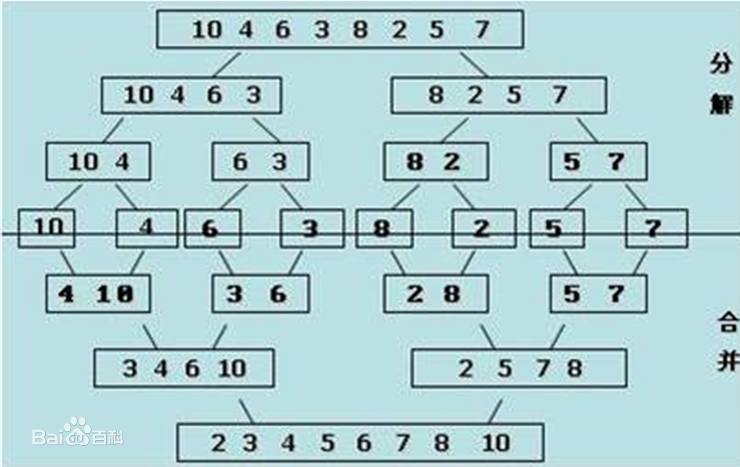
0x05 归并排序
归并排序(Merge Sort)的工作原理如下:
第一步:申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
第二步:设定两个指针,最初位置分别为两个已经排序序列的起始位置
第三步:比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
重复步骤3直到某一指针超出序列尾
将另一序列剩下的所有元素直接复制到合并序列尾
代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
public static int[] mergeSort(int[] nums) {
return mergeSort(nums, 0, nums.length - 1);
}
private static int[] mergeSort(int[] nums, int l, int r) {
if (l == r) return new int[]{nums[l]};
int mid = (l + r) / 2;
int[] lefts = mergeSort(nums, l, mid);
int[] rights = mergeSort(nums, mid + 1, r);
return merge(lefts, rights);
}
private static int[] merge(int[] nums1, int[] nums2) {
int len1 = nums1.length, len2 = nums2.length;
int index1 = 0, index2 = 0, index = 0;
int[] result = new int[len1 + len2];
for (; index1 < len1 && index2 < len2; ) {
if (nums1[index1] <= nums2[index2]) {
result[index++] = nums1[index1++];
} else {
result[index++] = nums2[index2++];
}
}
if (index1 == len1) {
System.arraycopy(nums2, index2, result, index, len2 - index2);
}
if (index2 == len2) {
System.arraycopy(nums1, index1, result, index, len1 - index1);
}
return result;
}
|
0x06 希尔排序
希尔排序的实质就是分组插入排序,该方法又称缩小增量排序。
原理
先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下(接近最好情况),效率是很高的,因此希尔排序在时间效率上比前两种方法有较大提高。
代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
public static int[] shellSort(int[] nums) {
if (nums != null && nums.length > 1) {
int len = nums.length;
for (int gap = len / 2; gap > 0; gap /= 2) {
for (int i = 0; i < gap; i++) {
for (int m = i; m < len; m += gap) {
int candidate = nums[m];
int n = m - gap;
for (; n >= 0 && nums[n] > candidate; n -= gap) {
nums[n + gap] = nums[n];
}
nums[n + gap] = candidate;
}
}
}
}
return nums;
}
|


